They think it's Mathematical... It is now.

Crucial differences in the way that football fans and mathematicians talk about probability

What does do we mean by ‘certain’? Photo by Pixabay: https://www.pexels.com/photo/soccer-ball-on-grass-field-during-daytime-46798/

It’s that time of the year when we’ve reached the end game of the football season. All across the country you will hear pundits talking about promotions, relegations, championships and European places. And in order to try to describe these situations you will hear phrases like “They’re not mathematically safe from relegation” or “They won’t relax until it’s mathematical”, using ‘mathematical’ as if it were a by word for ‘certain’.

Take Luton Town’s predicament, for example. They currently occupy 18^th place – the last relegation spot in the Premier League – with one round of matches to go. They are three points behind Nottingham Forest. A win in the Premier League is worth three points, while the losing team gets no points. On the last day of the season, if Luton win and Forest lose, the two teams will be tied on 29 points. The question of who gets relegated will then be decided by goal difference (the number of goals a team has scored minus the number they have conceded). Forest’s goal difference is bad. Having conceded 66 and scored just 47, their goal difference is -19. Luton’s is worse, at -31, reflecting the fact they have scored 50 goals but conceded 81.

Even if Luton were to catch Forest on points it seems unlikely that they’ll overhaul the goal difference gap of 12. For example, Luton would have to win 6-0 and Forest lose by the same scoreline (if the teams are tied on goal difference the team who has scored more goals finishes higher – which would be Luton). Unlikely, but not completely impossible.

And to be fair to pundits, they are recognising this possibility with phrases like “Luton’s survival is still a mathematical possibility” or “Luton’s relegation is not a mathematical certainty”, it’s just that the pedant in me wants to ask what other sort of ‘possibility’ is there? How can something be ‘certain if’ not characterised mathematically?

The answer is that there may be other sorts of ‘certainty’ – the certainty that comes with experience. The certainty that suggests that even though, with five games of the season to go, struggling Sheffield United could still have reached the 31 points needed to overhaul Nottingham Forest (on 30 points at that stage[1]), their record of just 16 points in the first 33 games (combined with the likelihood of Forest scoring more points) meant they were unfathomably unlikely to accumulate the required points in the handful of games remaining. This is the sort of ‘dead cert’ that might lure you into ‘betting your house’ on Sheffield United going down (if you were a betting person).

Although we might characterise ourselves colloquially as ‘certain’, in reality there is still a possibility, no matter how small, that Sheffield United could have stayed up. Consequently, and technically speaking, their relegation could not be considered a certainty (although they did, in fact get relegated, as was extremely likely!). However, this experiential perspective is not completely without mathematical merit. Indeed it is the basis of the frequentist view of probability.

In the frequentist interpretation, the probability of a given event occurring can be calculated by observing how many times that event occurs when we repeat a trial over and over again. For example, the trial might be rolling a die and the event might be observing a three. If you do enough trials (i.e. rolls) of a fair die, the probability of observing a three should level off at exactly 1/6 (there being six equally likely faces to choose from). In the figure below you can see how the probability, approximated from an increasing number of trials, levels off to around one sixth as the number of trials gets large.

Figure 1: The evolution of the approximation to the frequentist probability of throwing a three with a fair dice. Eventually the probability levels off at around one sixth.

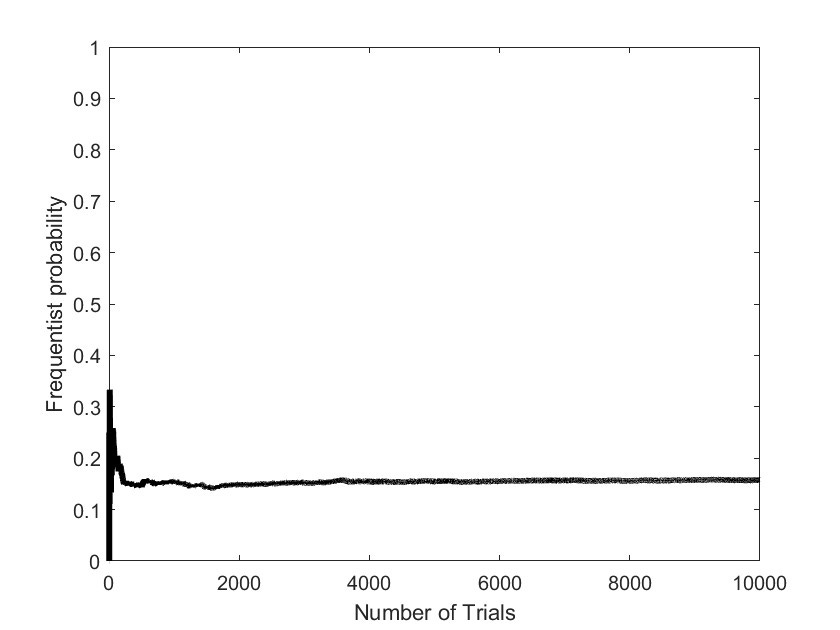
Here’s an example of how this frequentist view might influence our perceptions of the probability of an event. At Christmas, Sheffield United sat bottom of the table on just nine points. No team has ever beaten the drop from the Premier League having had just nine points at Christmas. Having seen no team survive relegation from 9 points on December 25^th (the event) in the 31 previous seasons of the Premier League (trials) gives the approximation to the frequentist probability of Sheffield United staying up this season as zero. Their relegation was a frequentist certainty.

It’s true that frequentist probabilities, also known as ‘long run probabilities’ are only considered appropriately accurate when taken over ‘many trials’. Whether the 31 previous Premier League seasons count as ‘many’ is not quite clear. In truth, just because it has not happened before, it doesn’t mean that no team with nine points at Christmas will ever survive. However, through this frequentist view, we can understand why, never having experienced it before, many football fans would have argued that Sheffield United’s relegation was a ‘certainty’.

Sometimes as a mathematician I think it’s important to step back and appreciate that the terms I take for granted in my day job can sometimes have a different meaning in the real world. In this case it’s important to recognise that outside my real of expertise, the ‘sure thing’ and the ‘dead cert’ don’t always have a probability of one.

---

[1] Nottingham Forest were docked four points for breaching Premier League profit and sustainability rules. This explains why it is possible for them to have a lower points total now, than they did earlier in the season.