The surprising bias in cancer survival rates

A Cancer Research UK report is telling us that cancer survival rates have improved, but by just how much?

Headlines have tended to focus on the more dramatic ‘improvements’ given by 10-year survival rates, risking painting a biased picture.

Cancer Research UK today published a report which highlights changes in cancer survival rates over the last 50 years. Many of the headlines (like the one above from the Guardian) have chosen to report the ‘doubling of cancer survival rates’ since the 1970s. The specific statistic these headlines are quoting is the ten-year survival rate, which the report says has increased from 24% in the 1970s to around 50% today. Indeed, five-year or ten-year survival rates are often quoted as key measures of cancer treatment success. The survival rate figures highlighted in the report are no doubt correct, but are they the right statistics to use to demonstrate improvements in cancer mortality rates?

Time-limited survival rates (typically given as five-, ten- and twenty-year) can improve because cancers caught earlier can be treated more successfully, but also because patients identified at an earlier stage of disease would naturally live longer, with or without treatment, than those identified later. The latter phenomenon is known as lead time bias, and can mean that statistics like five-year survival rates paint a misleading picture of the effectiveness of improvements in treatment and detection.

Lead time bias can make diagnosis/treatment programmes appear more effective than they actually are, when the perceived post-diagnosis survival time increases even if the course of disease progression is unaffected.

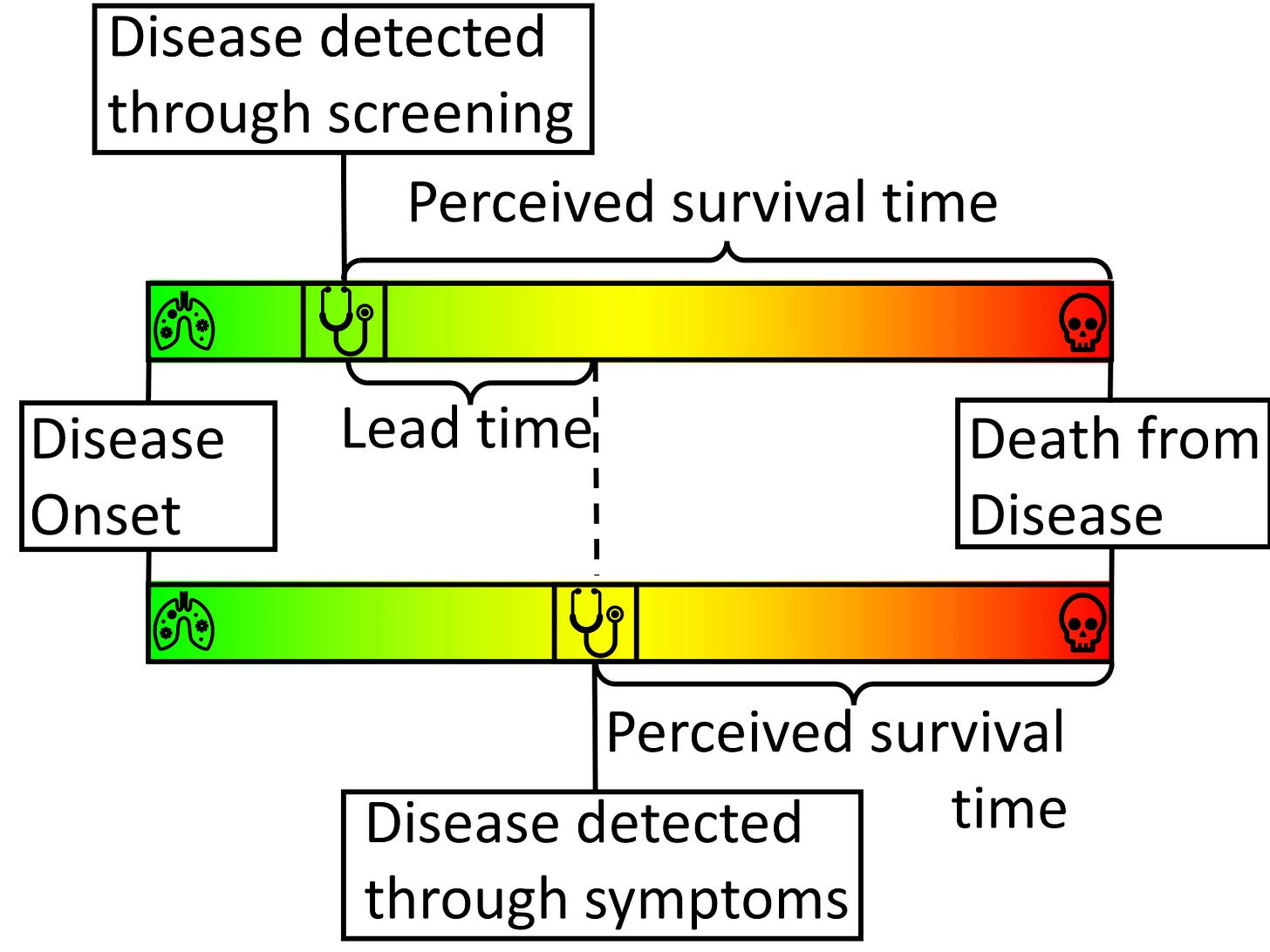
To illustrate the effect of lead time bias more concretely, consider a scenario in which we are interested in ‘diagnosing’ people with grey hair. Without a screening programme, greyness may not be spotted until enough grey hairs have sprouted to be visible without close inspection. With careful regular ‘screening’, greyness may be diagnosed within a few days of the first grey hairs appearing. People who obsessively check for grey hairs (‘screen’ for them) will, on average, find them earlier in their life. This means, on average, they will live longer ‘post-diagnosis’ than people who find their greyness later in life. They will also tend to have higher five-year survival rates. But treatments for grey hair do nothing to extend life expectancy, so it clearly isn’t early treatment that is extending the post-diagnosis life of the screened patients. Rather, it’s simply the fact their condition was diagnosed earlier.

To give another, more serious example, Huntington’s disease is a genetic condition that doesn’t manifest itself symptomatically until around the age of 45. People with Huntington’s might go on to live until they are 65, giving them a post-diagnosis life expectancy of about 20 years. However, Huntington’s is diagnosable through a simple genetic test. If everyone was screened for genetic diseases at the age of 20, say, then those with Huntington’s might expect to live another 45 years. Despite their post-diagnosis life expectancy being longer, the early diagnosis has done nothing to alter their overall life expectancy.

If time-limited survival rates are suspect because they engender lead time bias, what statistics should we be using instead in order to measure the benefits that improved treatment and earlier diagnosis have brought about? How can we demonstrate that we have genuinely become more effective at prolonging lives over the last 50 years?

The answer is to look at mortality rates (the proportion of people who die from the disease). Indeed such figures are given in the CRUK report: the rate at which people were dying from cancer in 2023 is 252 per 100,000 people, a fall of around 23% from where it was in 1973 at 328 per 100,000 people. There genuinely has been a substantial improvement since the 1970s but these mortality rates have generally failed to make the headlines because they paint a less dramatic picture of the improvements in cancer care over the last 50 years.

It’s also important to recognise that these absolute mortality risk figures aren’t definitive either. Since the 1970s we have also improved survival rates for diseases other than cancer. As we prevent people dying from other causes, and they consequently live longer, we would expect more people to get/die from cancer, typically at a later age. Controlling/adjusting these mortality statistics for age would, therefore, be an important qualification. Age-adjusted figures would likely paint a more positive picture of progress in preventing cancer than the raw mortality figures alone.

So while there is no doubt that cancer mortality rates genuinely have decreased over the last 50 years due to earlier diagnosis and improved treatments, describing the impact using five-year or ten-year survival rates tends to exaggerate the benefits.

This article is adapted from a piece originally published in The Conversation for which I was awarded the Royal Statistical Society’s “Best statistical commentary by a non-journalist” award.