The intriguing sequence completed by Liverpool’s title win
Why spotting patterns is important for scientific discovery and how coincidences can be misleading.
Liverpool have just clinched the Premier League title for the second time since the competition began (although it should be noted Liverpool have 18 other league titles bringing their total to 20). With it they have completed the beginning of a quite remarkable sequence, 33 years in the making. As can be seen in the table below, when ranked in order of titles won, from lowest to highest, the number of titles goes as follows 1, 1, 2, 3, 5, 8, 13.
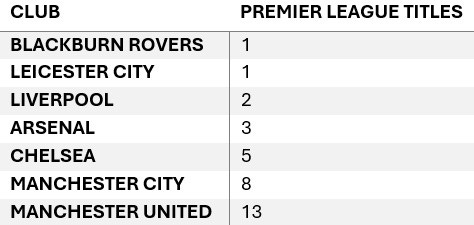
This sequence might not seem so significant to the untrained eye, but it will be enough to get many maths aficionados excited. They will recognise this as the Fibonacci sequence, in which each number (after the first two) is the sum of the previous two in the sequence. The sequence can be found in an astonishing array of places – from the spirals of seeds on sunflower heads and the bracts of pinecones to family tree patterns in some species of animals.
Fibonacci sequences (sequences in the plural because starting with a different pair of initial numbers and following the rule of adding consecutive numbers to generate the next gives you a different, but related sequence) were first introduced to European science in 1202 by Leonardo of Pisa, also known by his nickname Fibonacci (meaning son of Bonaccio).
Long before Fibonacci popularised the sequences in his book Liber Abaci, however, the sequences had been known to Indian Mathematicians. They had drawn upon the sequences to help them enumerate the number of possible poems of a given length, using short syllables of one unit duration and long syllables of two unit duration. The Indian poet/mathematicians knew that you could make a poem of length n by taking a poem of length n-1 and adding a short syllable or a poem of length n-2 and adding a long syllable. Consequently they figured out that to work out the number of poems of a given length you just had to add the number of poems that were one syllable shorter to the number that were two syllables shorter– the exact rule we use today to define a Fibonacci sequence.
Hidden in the sequences is another important and related mathematical mainstay – the golden ratio. As the terms in a Fibonacci sequence get larger, the ratio of each term to the one preceding it gets closer and closer to the golden ratio – approximated to 1.61803 by the first few places in its decimal expansion. The golden ratio is hypothesised to govern the arrangement of leaves on the stem of some plant species and supposedly leads to aesthetically pleasing results when applied in art, architecture and music.
Fibonacci sequences are often held up by mathematicians as exemplars of the beauty of mathematics. They can provide vivid visual examples of maths written into the patterns of the real world, without which many non-mathematicians can struggle to understand the elegance we see in our subject. In our over-enthusiasm to proselytize, however, there is a temptation to cast Fibonnacci sequences or the golden ratio as some sort of all-encompassing natural law governing phenomena across orders of magnitude, from the spiral shapes of nautilus shells to vortices of hurricanes to the curved arms of galaxies. In reality, although these natural features are aesthetically pleasing, very few of them conform to the rules of the Fibonacci sequence or exhibit the golden ratio. We must be careful that we don’t try to shoehorn every beautiful pattern into the delicate Fibonacci glass slipper - to suggest causation and impose meaning where there is none.
Coinscience
It’s extraordinary, then, to find the Fibonacci sequence cropping up in a place as unexpected as the Premier League. When, as scientists, we spot a well-known sequence like this appearing seemingly out of the blue, we should start to ask ourselves whether it tells us anything important about the process that generated the sequence. Is there some surprising unseen process underlying Premier League title battles or is it nothing more than a seemingly cute coincidence?
Spotting these sorts of seeming coincidences can be extremely useful for the process of scientific discovery. In 1912, for example, Alfred Wegener noticed the apparently strange coincidence that the coastline of West Africa and the eastern coastline of South America seemed to fit together like the pieces in a jigsaw puzzle. Despite the prevailing opinion at the time, that the enormous land masses which comprised the continents were just too big to move, Wegener proposed the only theory that reconciled his observations: continental drift suggested that the land masses weren’t rooted in place but could, ever-so-slowly, change their relative positions on the surface of the earth.
When he published his theory in 1915, he became a laughingstock. Geologists rejected his outlandish idea, citing a lack of mechanism for moving such enormous chunks of the Earth’s surface, dismissing the seemingly snug tessellation of the continents as pure coincidence. By the 1960s, however, the theory of plate tectonics – the movement of the solid mantle and crust over the Earth’s surface – gave credence to Wegener’s now widely accepted theories.
Elemental truths
In 1815, English physician William Prout noticed the fact that the atomic weights of the elements that chemist John Dalton had recently measured were roughly whole number multiples of the atomic weight of hydrogen. This led him to suggest that atoms of other elements would be amalgamations of various numbers of hydrogen atoms. For example, roughly eight grams of oxygen were needed to combine with one gram of hydrogen to make water. Since we know that every water molecule (H2O) contains two hydrogen atoms for every oxygen atom, by Prout’s theory, an oxygen atom should (and does) weigh around 16 times as much as a hydrogen atom. Based on similar, approximately whole number ratios for the other elements, Prout suggested that hydrogen was the only truly fundamental particle (which he dubbed ‘protyle’) and that atoms of other elements were made up of different numbers of hydrogen atoms.
Later, more accurate experiments showed that the weights of atoms of other elements were not close to being whole number multiples. Chlorine presented a particular problem. The formation of hydrochloric acid, HCl, comprising one atom of chlorine and one of hydrogen, required roughly 35.45 grams of chlorine to react with one gram of hydrogen. This suggested that chlorine atoms have an average weight 35.45 times that of hydrogen, casting serious doubt on Prout’s “whole number ratio” hypothesis.
Indeed, as it transpired Prout was not quite right. Atoms are, in fact, made up of protons, neutrons (which have almost exactly the same mass as protons) and electrons (which weigh around 2000 times less, meaning they make little difference in the calculations). There are also different versions of the same element called isotopes which have the same number of protons, but different numbers of neutrons. Chlorine for example has two main isotopes, one with 17 protons and 18 neutrons and, therefore, a mass of roughly 35 times that of a hydrogen atom and another with 17 protons and 20 neutrons and a mass roughly 37 times that of a hydrogen atom. 35Cl and 37Cl occur in a ratio of roughly three-to-one, explaining why approximately 35.5 (¾ x 35+¼ x 37) grams of naturally occurring chlorine was needed to combine with one gram of hydrogen. Despite this nuance, when considered for each isotope, Prout’s suggestion that the mass of other atoms would be roughly integer multiples of the mass of a hydrogen atom was correct and became known as the ‘whole number rule’ for which Francis Aston, who articulated it in this form, was awarded the 1922 Nobel Prize in Chemistry.
Perhaps more importantly, by spotting a pattern in the noisy measurements, Prout’s insight served to stimulate the academic debate which led to significant improvements in our understanding of atomic structure. When, over 100 years later, Ernest Rutherford fired alpha particles at nitrogen atoms to displace hydrogen nuclei, he conjectured that all atoms might be made up of these fundamental particles. He went on to name them protons, which, as well as deriving from the Greek word protos meaning ‘first’, satisfied Rutherford’s additional intention of honouring Prout for his insightful conjecture.
The evolution of a mistake
Although coincidences can point the way to new scientific discoveries, they can also prove an obstacle to scientific progress when they appear to confirm an incorrect theory. In the early 1800s German anatomist Johann Friedrich Meckel made just such a blunder. He was a believer in scala naturae (the ladder of nature) in which humans sit above all other animals in an ordered but static hierarchy. The simplest, most primitive life forms were supposed to sit on the lowest rungs of the ladder, while the most complex and advanced beings resided on the highest. His views were hardly surprising given that this ‘great chain of being’ was the predominant theory of the day. The now generally accepted theory of ‘common descent’ – that multiple species descend from a single ancestral population - was only in its infancy as an idea at the time.
Meckel employed scala naturae to come up with a conjecture about his area of speciality - embryonic development. Known as recapitulation theory, he posited that, as they developed, the embryos of higher order animals (like mammals) progressed successively through forms which strongly resembled the ‘less perfect’ animals, like fish, amphibians and reptiles, on lower rungs of the ladder. One startling, but seemingly unlikely prediction of this theory was that, as humans progressed through the ‘fish stage’, their embryos would have gill slits.
As it happens, it was discovered in 1827 that human embryos really do have slits that resemble gills at an early stage of development. This extraordinary finding seemed to bear out Meckel’s prediction and corroborate his recapitulation theory. So strong was the perceived evidence that the theory became widely accepted, and it wasn’t until almost 50 years later in the 1870s that the recapitulation theory of development was finally put to bed for good as the idea of common descent started to take hold. Common descent made it clear that, far from undergoing a ‘fish stage’ in the womb, the gill slits were a consequence of the fact that, sharing a common ancestor with fish, we also share much of their DNA and early developmental processes. Sometimes coincidences can lead scientists astray, seeming to point to one conclusion when, in fact, there is an alternative explanation for the observations that is better supported by the facts.
So what does the fact that the beautiful, almost mystical Fibonacci sequence has cropped up in the data on the number of Premier League titles mean for the beautiful game? With no plausible mechanism which could have given rise to the sequence, the answer is almost certainly nothing. It’s wonderful to have spotted this seemingly unlikely coincidence, giving us a chance to reflect upon the importance of Fibonacci numbers. However, just like Meckel’s gill slits, its appearance in the Premier League records is nothing more than a spectacular but ultimately misleading coincidence.
A version of this piece appaeared on BBC Future and is adapted from text in my second book How to Expect the Unexpected.



I would postulate that there could be a relationship between previous winners and later winners - winning often breeds success and fortune.
The more a team wins the more it's likely to cement its place in the winners pantheon. They can afford and attract the best players etc, and as you look down the final tables you will see an ordered list of financial muscle and attractiveness to players and overseas fans.
Perhaps there's a multiplier effect from success?
It would be interesting if we see the same effect in other sports leagues, business success in sectors etc?