The counter-intuitive mathematical phenomenon hiding at the Men’s Under-21 Euros
The birthday problem is a timeless mathematical trick that surprises almost everyone when they first hear it.

The men’s under-21 Euros climaxes this evening when Lee Carsley’s reigning champions England take on fierce rivals Germany. The path to defending the title hasn’t been without setbacks for the young Englishmen, losing their final group game earlier in the tournament to the same opposition that they face tonight. The whole tournament swings on the question of whether or not they will be able to exact their revenge this evening, or whether their opponents can prevail over them for a second game in a row; this time in order to lift the trophy.
Putting aside the importance of tonight’s result for a moment, the Euros offers a rare opportunity to test out an old but surprising piece of mathematical lore. The ‘Birthday problem’ or ‘Birthday paradox’, as it is sometimes known, asks ‘How many people do you need to assemble before it becomes more likely than not that a pair of people in your group will share a birthday?’ The answer is surprisingly few – just 23 in fact.
If this is the first time you are hearing this then I don’t blame you if you’re a little sceptical of my claim; 23 seems far too few. Afterall, there are 365 days in most years (366 in a leap year) – 365 different possible days that people’s birthdays could fall on, so it feels, intuitively, that the number should be more like 180-ish, somewhere around half the number of days in the year.
The problem with this reasoning, sadly, is that it is too self-centred. We tend to put ourselves in the shoes of one of the people in the room and think about how many other people we would need to find a match for our specific birthday. But this is the wrong way to go about it. Instead we need to think about the total number of pairs of people in the group – finding pairs of matching birthdays, after all, being what the problem is all about.
To figure this out we can think about how many unique handshakes there would be between people in the room if they were all to shake hands. We could get the first person to shake hands with the 22 others. Then the next could shake hands with the 21 they haven’t yet shaken with, the next with the remaining 20 and so on. This then continues down to the penultimate person who just shakes hands with the last person – the only person they have yet to shake hands with. If you add up all these handshakes (22 + 21 + 20 + … 3 + 2 + 1) it transpires that in a room of just 23 people there are 253 distinct pairs of people (see Figure 1).

If we assume that birthdays are evenly spread throughout the year (not quite true – but good enough for us for now) with a little bit more maths (you can check out the details in my first book The Maths of Life and Death) tells us that, with that huge number of pairs of people, the probability of one person having a birthday that matches someone else’s is just over half – more likely than not.
‘How does this relate to the Men’s Under-21 Euro finals?’ you might well ask. Well, it turns out that each of the squads that began the tournament comprised 23 (the magic ‘birthday number’) players – each of whose birthdays is readily accessible on the internet. This provides the ideal opportunity for us to test out our mathematical birthday theory and to see whether it holds in reality. If the maths holds up then we would expect around half of the 16 squads to contain two or more players who share a birthday.
If you were to scrape the dates of the (23 x 16) = 368 different players’ birthdays and then to do the (253 x 16 =) 4048 pairwise comparisons of birthdays of players in the same squad as each other, then you would find something quite remarkable. (Don’t worry, I’ve done it for you).
An unexpectedly large, 11 (Czechia, France, Georgia, Germany, Italy, Netherlands, Poland, Romania, Slovakia, Spain, and Ukraine) of the 16 squads have at least two players who share the same birthday – only 5 squads have no matching birthdays. Remember the maths predicts there should, on average, be 8 (if we were to repeat the experiment enough). In these Under-21 squads, matching birthdays are even more common than we might expect on average.
Looking into the details it turns out that, remarkably, three countries (Germany, Italy and Ukraine) have two pairs of players who’s birthdays match. For finalists Germany, Ansgar Knauff and Nnamdi Collins share a birthday on 10th January while Nelson Weiper and Nahuel Noll both celebrate their birthdays on St Patrick’s day – 17th March.
But get this – Georgia have three players born on the same date – 15th January – while Czechia have three separate pairs of players who share birthdays on 15th February, 18th May and 13th July. But as far as birthday coincidences go, Spain really take the honours in this Euros competition. Not only do they have Gerard Martín and César Tárrega who share their birthday on 26th of February, and Pablo Marín and Roberto Fernández who both celebrate on 3rd July, but they also have a triplet of players in Diego López (born 2002), Javi Guerra (born 2003) and Juanma Herzog (born 2004) who all came into the world on 13th May. The pair of Gerard Martín and César Tárrega were even born on exactly the same day of the same year - 2002.
Why are there so many more players who share a birthday than the maths predicts? Well it turns out that there is a well-supported theory, in the UK at least, that suggest that children who are born towards the start of the school year (i.e. the autumn) enjoy the advantage of being more physically and mentally developed than their peers born later. This so-called relative age effect (RAE) gives them a boost when it comes to being picked for school and extracurricular sports teams, which ensures that this head-start is reinforced – the more physically developed children get more practice, more coaching and more opportunities for physical development, which further enhances their advantage.
In many of the countries of Europe, although the school year starts at roughly the same time as in the UK, the cut-off date is different. Instead of segregating children based on the 31st August back-to-school date, many countries instead use the New Year as a cut off. This ensures that all the children in a school year are in fact also born in the same calendar year. Consequently, the sporting advantage conferred by being the oldest in the year group is weighted more heavily towards those born early in the New Year, with the autumn babies now being amongst the more disadvantaged.
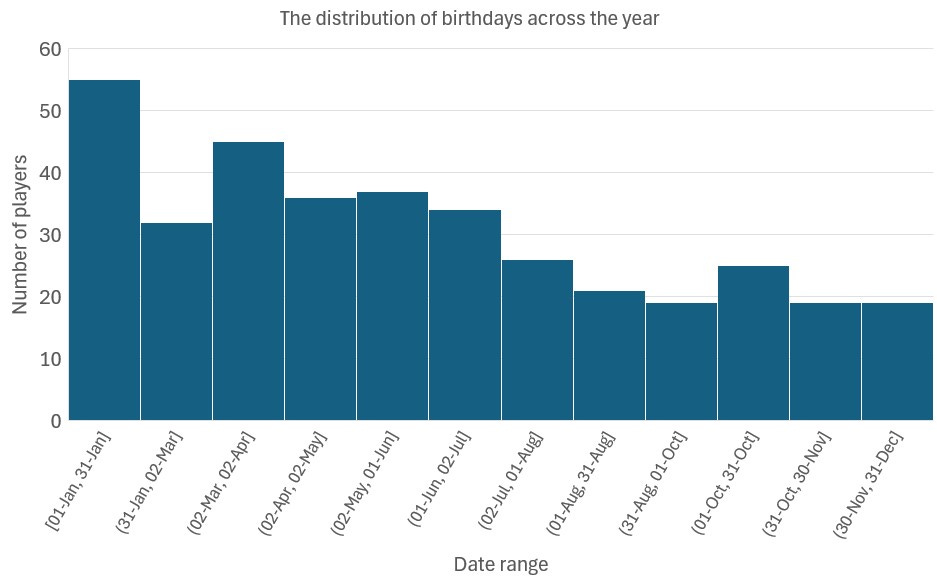
This bias, amongst professional sports people, towards being born earlier in the year, is clearly visible in the Under-21 Euros birthday data (see Figure 2). All of the five most popular birthdays (each being shared by five players) fall in the first half of the year with three of them falling in January alone.
Why does this make a difference to the Birthday problem? Well, remember that earlier I said that the assumption that birthdays were evenly spread throughout the year was ‘good enough’ for our purposes. In fact, the uneven spread of birthdays does make a difference to the calculation. If you account for birthdays being more bunched up, this makes the probability of finding a match even more likely in a fixed group size. Because there is a bias in the birthdays of the elite sportsmen who take part in this Euros, we tend to see more birthday matches than the naïve theory we outlined above would predict. In these sorts of cohorts you need even fewer than 23 individuals in a group for the chances that two of them will share a birthday to become more likely than not.
Looking at the Euro Under-21 squads provides some evidence about the surprisingly likelihood of calendrical coincidences hinted at by the basic birthday problem maths. However, it also exposes some of the nuances in the assumptions underlying the calculation, indicating that these sorts of coincidences might be more likely even than the original surprising theory suggests.
What it doesn’t do is help us to understand who will win tonight’s final. Counting up the number of birthday pairings, we can see that Germany beats England by a scoreline of two pairs to nil. Many England fans, including myself, will be hoping that this same scoreline isn’t repeated on the pitch in Bratislava this evening.



