That time when 133 people won the lottery on the same day
It's the 30th anniversary of a seemingly miraculous occurrence - when 133 people shared a 16 million pound roll-over jackpot.
The fourteenth of January 1995 was just the ninth time the United Kingdom’s National Lottery had been drawn. A week before, the eighth draw had ended with no one matching all six numbers. For just the second time in its history, the prize money rolled over to the following week, giving an enticing jackpot of £16,293,830. By the time the day of the draw came around, 70 million tickets had been sold – more than one for every person in the country, let alone the adults who were actually eligible to play. Large swathes of the nation were buzzing in anticipation of that evening’s draw.
Can you imagine the feelings as you watch the draw live on TV and the numbers come out. After seeing two of your numbers (23 and 38) plucked from the drum, a third – number 17 – comes out as well. you are guaranteed a prize, which will pay back all the stakes you’ve sunk into the lottery so far. But then comes a fourth, lucky number 7, and a fifth, number 32; and finally, a sixth number to match the remaining one on your ticket – 42 - the answer to the Ultimate Question of Life, the Universe, and Everything. You’ve won the jackpot.
Sadly for everyone who experienced it, that scene played out 133 times across the country that night. 133 people had each independently chosen the numbers (in ‘ascending numerical order’) 7, 17, 23, 32, 38 and 42. Can you now imagine the feeling of having to confront this brutal reality; that instead of 16 million pounds all to yourself, you have to split the jackpot with 132 others who’d matched all six numbers. Each of that evening’s winners took home just £122,510 – still a large sum of money, especially back in 1995, but nothing compared to the prize each had thought they would receive when they first realised they had won. Gutted doesn’t cut it.
Why had so many people picked the winning numbers for the draw in which won them just a 133rd share of the jackpot? The answer, as I discovered in my second book - How to Expect the Unexpected - comes down to the fact that we are so poor at being random. Intuitively we think of random as being well spaced, so when we are asked to generate a random pattern ourselves, an even spread is often what we go for.
When the winning numbers are marked on the National Lottery play slip, shown in the left-hand panel of the figure below, several things quickly become apparent. Firstly, none of the numbers are adjacent to each other. That preconception that randomness somehow means spaced out seems to make consecutive numbers or clusters of numbers seem unlikely. Surely, we reason, dispersed sets of numbers are more likely to come up than six consecutive numbers. Indeed, dispersed picks are far more likely to be drawn than six consecutive numbers. It’s tempting to conclude, then, that all choices with consecutive numbers should be avoided, but this reasoning fails. Well-spaced picks only occur more often because there are so many more well-spaced combinations than sets of six consecutive numbers. No single well-dispersed pick is any more or less likely to come up than any other set of six numbers, consecutive or otherwise. As it turns out, mathematics dictates that almost exactly half of all draws in a six-from-forty-nine lottery (choosing six numbers from 49 balls as in the original incarnation of the UK’s national lottery) should contain at least one pair of consecutive numbers.
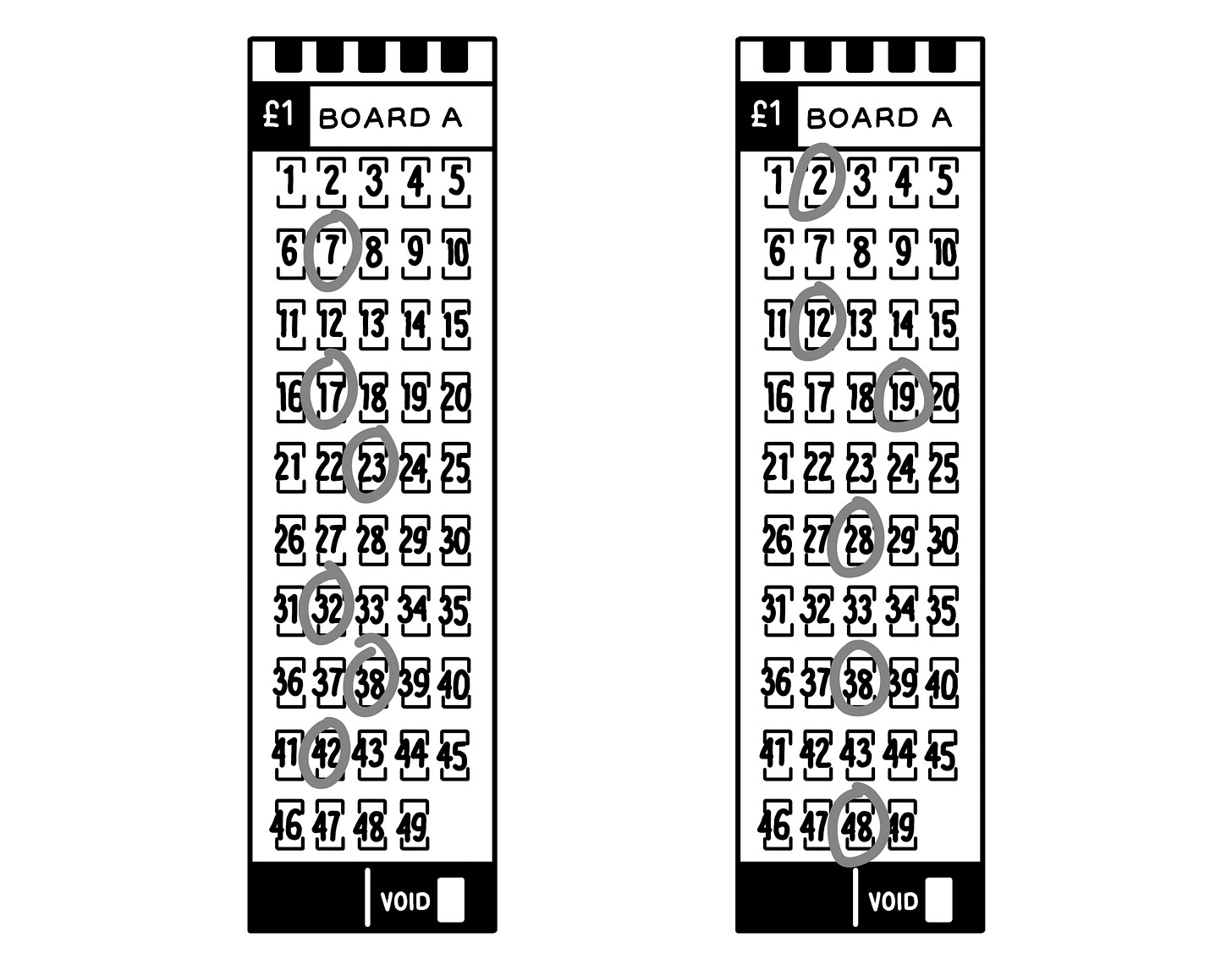
The second thing to note from looking at the play slip is that each number is on a different row, but none of them is immediately above or below one another. This, perhaps, is because although we imagine randomness as being well distributed, completely regular spacing doesn’t seem very random either, so small variations from a regular pattern help us to convince ourselves we are being random.
Thirdly, it’s apparent that none of the numbers is drawn from the outer columns of the play slip. In fact, for this draw, all the numbers are drawn from just the second and third columns. This might be an effect of the so-called middle bias , which suggests that people filling in multiple-choice answer sheets – not dissimilar to the lottery play slip – tend to favour the middle columns when guessing ‘at random’.
When combined, these three factors, along with the fact that the world’s favourite number (7) was part of the winning draw, probably contributed to the over-representation of the fateful numbers in players’ choices. And if the most-shared jackpot wasn’t enough to convince you of these biases, how about the second-most distributed top prize? On 16 March 1996, fifty-seven people won with the numbers 2, 12, 19, 28, 38 and 48. Plotting them on the play slip in the right panel of the figure above illustrates exactly the same three principles.
By analysing the frequency with which jackpot-winning numbers are picked, researchers at the University of Southampton were able to demonstrate that all three of these biases are genuinely in play when people choose their lottery numbers. They also confirmed the well-established proclivity for people to use birthdays as their picks – choosing the numbers between one and thirty-one with greater frequency than those above thirty-one. Picking according to these unwritten subconscious rules significantly reduces your expected winnings, precisely because you may have to share any prize you win with lots of other people. Choosing numbers purely at random is a better idea, but your expected returns are still only a meagre 55p for every pound you spend.

Although there’s nothing you can do to increase your chances of winning the jackpot, there is a way to improve your chances of taking home as much of the prize as possible if you do win. Actively taking advantage of other people’s randomness biases and choosing ‘unpopular’ sets of numbers can improve your expected returns to over 90 pence in the pound. Still a loss, but a much smaller one than if you inexpertly try your hand at being random. Appreciating that we, as a species, are not very good at being random is the first step along the road to being able to recognise and avoid the fate of others who draw too readily on their misconception of randomness being evenly spread and unclustered.




