'How can you give yourself the best chance of finding the best partner?

How can you use maths to optimise your love life; and is it really the best tool?

Photo by Irina Iriser: https://www.pexels.com/photo/photography-of-red-rose-plant-1122639/

This week it’s Valentine’s day. A day for star-crossed lovers to reaffirm their adoration and for secret admirers to dare to gift the objects of their desires a token of their affection. I will admit that I don’t buy into Valentine’s day. My jaded older self would tell you that it’s an overly-commercialised made-up ‘celebration’, for which greeting card companies have convinced us that the appropriate way to express our sentiments is through gifting the mass-produced tat that they flog us for extortionate prices.

But I was not always this cynical. One year I bought 30 bunches of daffodils and strung them up on lamp-posts and notice boards that marked my girlfriend’s route home. Every surface in our flat was covered with jars and cups full of the chirpy yellow flowers. Incidentally this was also the year I discovered I had hay fever! It is surprisingly hard to give away 30 bunches of daffodils the day after Valentine’s.

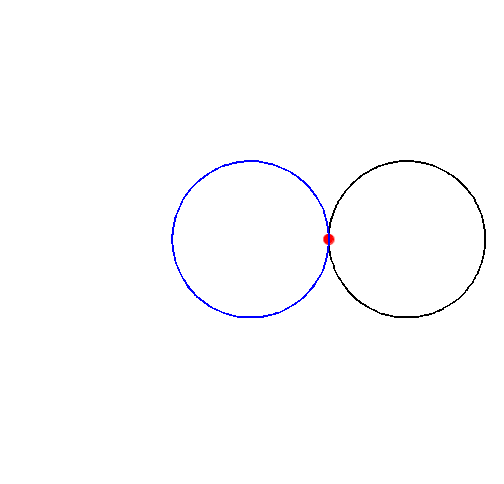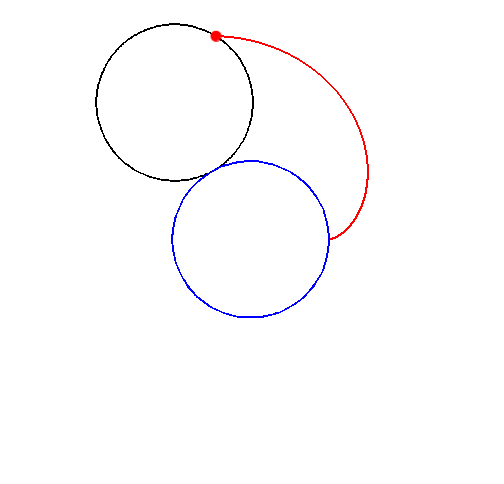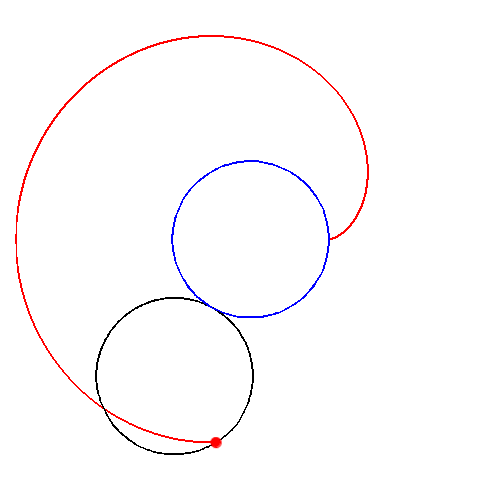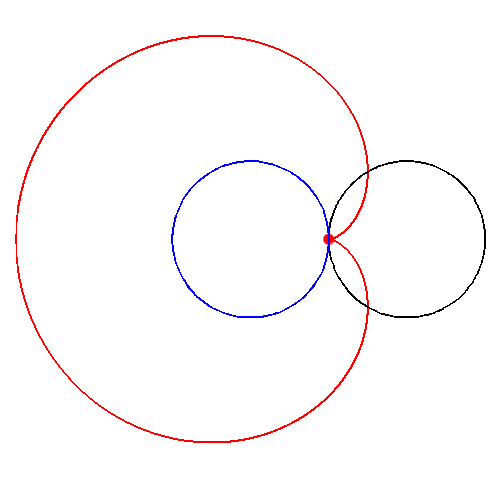
Before the daffodil debacle, when I was still at school studying further maths, one Valentine’s day I sent my girlfriend the equation (x² + y²)² + 4ax(x² + y²) - 4a²y² = 0, in a card which asked her to plot it on her graphical calculator. The equation plots out a curve known as a cardioid – a heart shaped curve. Let it not be said that love does not encroach into the world of mathematics.

The Cardioid curve can be generated by tracking a fixed point on a circle as it rolls around another circle of the same radius. This file is licensed under the Creative Commons Attribution-Share Alike 4.0. International license. Author: AtomicShoelace

Conversely, mathematics itself has something to say about the world of love. Purportedly it can give you the best chance of finding the best partner. We will come back to this, but let’s tackle a less consequential problem first. What if you want to take your Valentine’s date out for a nice meal? You’re both quite hungry, but you’d like to find somewhere nice. You don’t want to dive into the first place you see. You consider yourself a good judge, so you’ll be able to rank the quality of each restaurant relative to the others. You figure you’ll have time to check out up to 10 restaurants before your date gets fed up with traipsing around. Because you don’t want to look indecisive, you decide that you won’t go back to a restaurant once you have rejected it.

The best strategy for this sort of problem is to look at and reject some restaurants out of hand in order to get a feel for what’s out there. Once you’ve judged a number of restaurants you can choose the first one you see that’s better than all the others you’ve looked at so far.

This is called an optimal stopping strategy. Once you’re happy with the strategy, the question becomes, how many restaurants should you look at and reject, just to get a sense of what’s on offer? If you don’t look at enough then you won’t get a good feel for what’s available, but if you rule out too many before taking the plunge then your remaining choice is limited.

The strategy is to assess, but reject, every option up to a given cut-off point (dashed line) and then accept the next option you evaluate which is better than all the previous options.

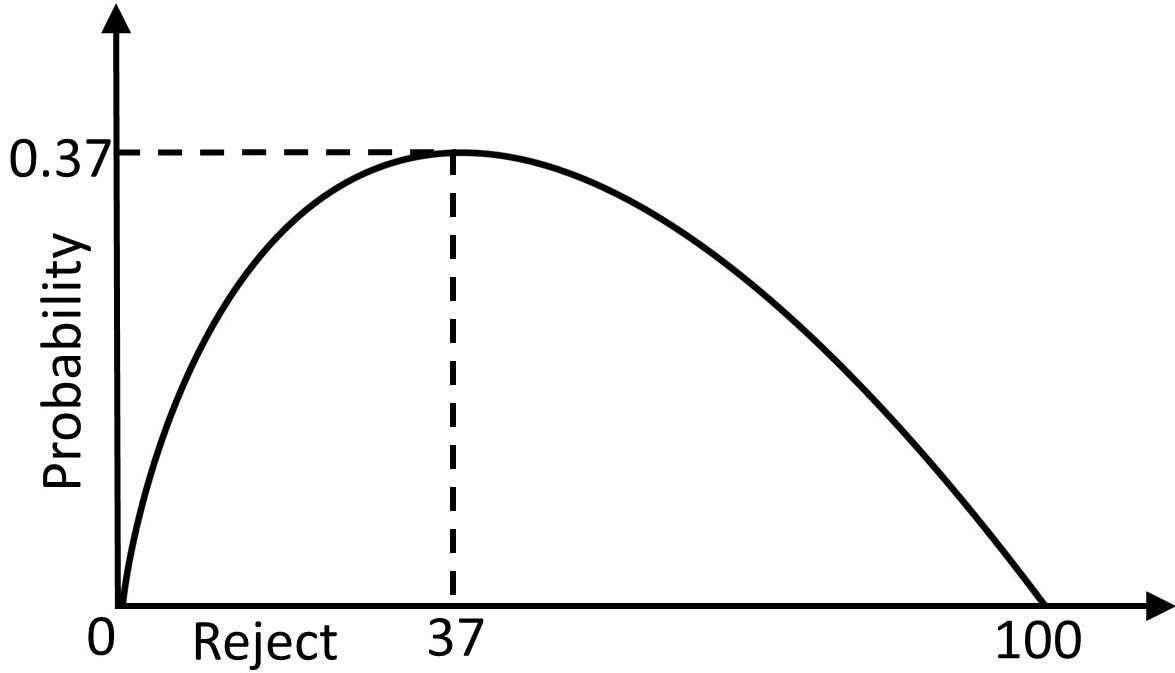
The maths behind the problem is complicated, but it turns out you should judge and reject roughly the first 37% of the restaurants (rounded down to 3 if there are only 10) before accepting the next one that is better than all the previous ones. More precisely, you should reject the fraction 1/e of the available options, where e is a mathematical shorthand for a number known as Euler’s number. Euler’s number is approximately 2.718, so the fraction 1/e is roughly 0.368 or, as a percentage, approximately 37%.

But what if the best restaurant was in the first 37%? In this case you miss out. The 37%-rule doesn’t work every time: it’s a probabilistic rule. In fact, this algorithm is only guaranteed to work 37% of the time. That’s the best you can do given the circumstances, but it’s better than the 10% of times you would have chosen the best restaurant if you had just picked the first of 10 at random, and way better than the 1% success rate if you had to choose at random between 100 restaurants. The relative success rate improves the more options you have to choose from.

The probability of choosing the best option is maximised when we judge and reject 37% of the options before accepting the next one we assess that is better than all those we have previously seen. In this scenario, the probability you choose the best restaurant is 0.37 or 37%.

The optimal stopping rule doesn’t just work for choosing restaurants. You can use it to get the best seat on the train or to choose the shortest queue at the supermarket. And if you’re clinical enough, you can even use this algorithm to tell you how many people to date before you decide to settle down.

You first need to decide how many partners you think you might get through by the time you’d like to get out of the dating game. Perhaps you might have one partner a year between your 18^th and your 35^th birthdays, making a total of 17 potential partners to choose from. Optimal stopping suggests that you play the field for about six or seven years (roughly 37% of 17 years) trying to gauge who’s out there for you. After that you should stick with the first person who comes along who’s better than all of the others you’ve dated so far.

Understandably, not many people are comfortable with letting a predefined set of rules dictate their love life. What if you find someone you’re truly happy with in the first 37%? Can you really cold-heartedly reject them because you’re on an algorithmic love mission? What if you follow all the rules and the person you decide is best for you doesn’t think that you’re the best for them? What if your priorities change half way through?

Fortunately, in matters of the heart, as with other more obviously mathematical optimisation problems, we don’t always need to look for the very best solution, the single person who is the perfect fit – The One. There are likely to be multiple people out there who will be a good match and with whom we can be happy. Optimal stopping doesn’t hold the answers to all of life’s problems.